أشكال في الحياة

عن الأشكال

مثلث

من الممكن تصنيف المثلثات تبعا لاطوال اضلاعها كما يلي:

• مثلث متساوي الأضلاع: هو مثلث أضلاعه متساوية. جميع زوايا المثلث متساوي الاضلاع متساوية أيضا، وقيمتها 60 درجة.
• مثلث متساوي الضلعين: هو مثلث فيه ضلعان متساويان. الزاويتان المقابلتان لهذين الضلعين تكونان متساويتان أيضا.
• مثلث مختلف الأضلاع: هو مثلث أطوال أضلاعه مختلفة. زوايا هذا المثلث تكون مختلفة القيم أيضا.

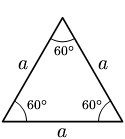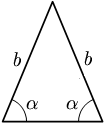متساوي الاضلاع	متساوي الساقين	مختلف الاضلاع

كما يمكن تصنيف المثلثات تبعا لقياس أكبر زاوية في المثلث:

• مثلث قائم: له زاوية قياسها 90 درجة (زاوية قائمة)، يدعى الضلع المقابل للزاوية القائمة بالوتر، وهو أطول أضلاع هذا المثلث.
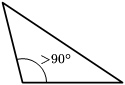
• مثلث منفرج الزاوية: له زاوية قياسها أكبر من 90 درجة واصغر من 180 درجة(زاوية منفرجه)
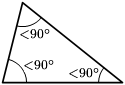
• مثلث حاد الزوايا: كل زواياه قياسها أصغر من 90 درجة (زاوية حادة).

nbsp;

المخروط

المخروط في علم الهندسة، هو شكل مجسّم تستقر قاعدته على سطح مستو ومحدّد بمنحنى مغلق يُسمى الخط الدليلي. ويتكون السطح الجانبي للمخروط من كل أجزاء الخط الواصل بين نقطتي الخط الدليلي إلى رأس المخروط، وهي نقطة محددة ليست على مستوى القاعدة. وعندما يكون الخط الدليلي دائرة، يسمى المخروط المخروط الدائري. وعندما تكون أجزاء الخط الواصل من قمّة الرأس إلى مركز الدائرة عموديًة على مستوى القاعدة، يسمى المخروط المخروط الدائري القائم. وإذا قطعنا المخروط الدائري القائم بمستوى لا يشمل رأسه، فإن المقطع الناتج يسمى المقطع المخروطي. والدوائر والقطع الناقص والقطع الزائد والقطع المكافئ كلها قطاعات مخروطية.

وارتفاع المخروط هو الخط العمودي من قمة رأس المخروط إلى سطح القاعدة. وطول المخروط هو ارتفاع المخروط نفسه. كما أن حجم المخروط (ح) يمكن إيجاده باستعمال القانون:

ح= 1/3 م ع

حيث (م) ترمز إلى مساحة القاعدة و(ع) إلى ارتفاع المخروط. وإذا كانت قاعدة المخروط دائرة فتكون م= ط نق²، حيث نق هو نصف قطر الدائرة، (ط) النسبة التقريبية وتساوي 3,1416، ويكتب قانون الحجم عندئذ كما يلي:

ح = 1/3 ط نق²ع

وفي المخروط الدائري القائم، نجد أن جميع الخطوط (من قمة الرأس حتى الخط الدليلي) لها طول واحد يسمى الارتفاع الجانبي. ومساحة السطح الجانبي (س) للمخروط الدائري يمكن أن تحسب باستعمال القانون التالي:

س= ط نق ل

وفي هذا القانون، فإن نق يرمز إلى نصف قطر القاعدة، ويرمز ل إلى الارتفاع الجانبي. والمساحة الكلية لسطح المخروط تساوي المساحة الجانبية للسطح مضافة إليها مساحة القاعدة.

وإذامرَّ سطح مستو مواز للقاعدة بين قمة رأس المخروط وقاعدته، فإن المخروط ينقسم إلى مخروط أصغر وشكل مجسم يسمى المخروط الناقص. ويساوي حجم المخروط الناقص حجم المخروط الأصلي مطروحًا منه حجم المخروط الأصغر.

متوازي مستطيلات

متوازي المستطيلات

في الهندسة الرياضية، يطلق اسم متوازي المستطيلات (بالإنجليزية: cuboid‏) على الشكل الصلب الذي يحيط به ست مستطيلات من جميع جهاته. وهو مكعب مستطيل. تكون جميع زواياه قائمة، وتكون الأوجه المتقابلة متساوية. كما يمكن اعتباره موشور بزاوية قائمة.

إذا كانت أبعاد متوازي المستطيلات هي a,b,c عندها يكون حجمه يعطي بالعلاقة abc ومساحة سطحة الخارجي بالعلاقة 2ab + 2bc + 2ac. كما يعطى طول القطر الثلاثي الأبعاد بالعلاقة:

مكعب

هذه المقالة عن المكعب في الهندسة الرياضية. لتصفح عناوين مشابهة، انظر مكعب (توضيح).

المكعب Cube جسم له ستة أوجه منتظمة الشكل, وكل هذه الأوجه هي مربعات, فالمكعب هو كتلة تكون بمجملها زوايا قائمة ويكون فيه العرض والعمق والارتفاع متساوية.

حافات المكعب هي خطوط مستقيمة وأركانه تشكل زوايا قائمة.

المكعب له ثمانية أركان واثنا عشر حافة(حرف) وستة أوجه.

ويقدر حجم المكعب بطول حرفه مضروبا بنفسه ثلاث مرات, أي مكعب أحد أحرفه.

وتقدر مساحة أوجهه بستة أضعاف مساحة أي وجه فيه, أي ستة أضعاف أحد أحرفه.

دائرة